Method of molecular dynamics
The MD method is suitable for a variety of classical problems (it can be used in mechanics, thermodynamics, etc.). The distinctive feature of MD is the fact that classical mechanics is used to describe the motion of particles. Interatomic forces can be represented in the form of classical potential forces (as the gradient of the potential energy of the system).
The molecular dynamics (MD) method in physical modeling belongs to the so-called deterministic methods. This means that the state at the next moment in time ![]() is completely determined by the current state
is completely determined by the current state ![]() . Thus, in order to determine the state of the system at any moment in time, it is sufficient to specify the initial conditions and the general rules or regularities of the system's evolution.
. Thus, in order to determine the state of the system at any moment in time, it is sufficient to specify the initial conditions and the general rules or regularities of the system's evolution.
Some classical problems for which the MD method is used include the Kepler problem (the problem of celestial bodies' motion), modeling of ideal or real gases, the flight of a body thrown at an angle to the horizon, oscillatory problems, and many others.
The limitations of the MD method are evident: it does not describe quantum effects in thermodynamics, and it is not suitable for relativistic velocities in mechanics.
The most common use of the MD method is Euler schemes.
Let at the moment in time ![]() the particle has coordinates
the particle has coordinates ![]() , velocity projections
, velocity projections ![]() , and force projections
, and force projections ![]() . It is required to determine these parameters at the moment in time
. It is required to determine these parameters at the moment in time ![]() . Let's use "school" mechanics:
. Let's use "school" mechanics:
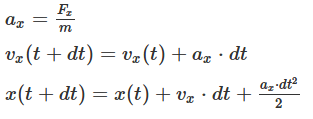
It is clear that for other projections (for example, ![]() , etc.) there will be similar formulas.
, etc.) there will be similar formulas.
In some cases, the last term in the expression is not taken into account, assuming that ![]() , and sometimes the opposite is true:
, and sometimes the opposite is true: ![]() . These nuances will be considered later on specific examples.
. These nuances will be considered later on specific examples.
If forces are determined by potentials, then
![]()
where U is the potential at the point where the particle is located.
The MD method has an error that is due to the fact that the term of the form something * dt is linear, while the physical quantity can change nonlinearly. For more details on this, see the mathematics course - on the differences between the derivative of a function and its differential.