Building bubbles, squares, etc. (QT, similar to TChart Bubbles)
It so happened that there is no ready-made component for drawing bubbles in QwtPlot - like, for example, in TChart from Borland (Delphi). But it's no problem. All this can be done manually, and it's not very difficult.
If you don't care about the scale of the bubble relative to the qwt plot, you can use the QwtSymbol class. To do this, you first need to plot points in QwtPlotCurve (I recommend to read this here first):
#include "qwt_plot_curve.h"
#include"qmath.h"
QwtPlotCurve *curve = new QwtPlotCurve; QVector<QPointF> *points = new QVector<QPointF>; for (float i=0; i <= 10; i += 0.1) points->append(QPointF(i, qSin(i))); curve->setSamples(*points); curve->attach(ui->qwtPlot);
And to disconnect the automatic connection of the curve's points with lines, we add:
curve->setStyle(QwtPlotCurve::Dots);
Now let's create a symbol:
#include "qwt_symbol.h"
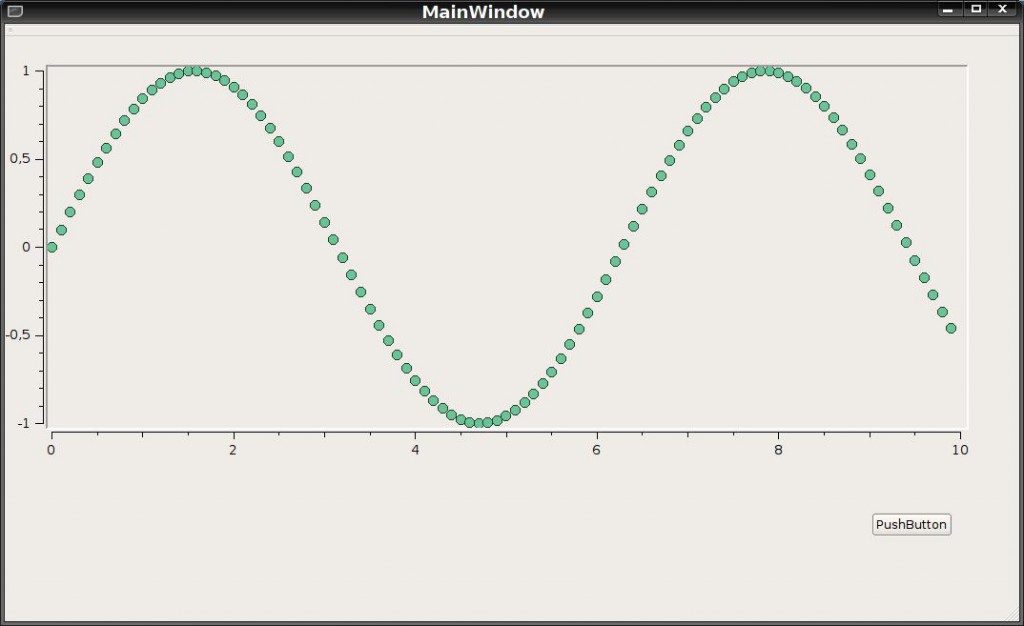
QwtSymbol *symbol = new QwtSymbol; symbol->setStyle(QwtSymbol::Ellipse); // set the style - in this case - circles symbol->setSize(10); // set the size in pixels
Now we attach the symbol to the curve:
curve->setSymbol(symbol);
You can pass different arguments to the setStyle method - to create circles, squares, crosses, hexagons, etc.: QwtSymbol::Cross (crosses), QwtSymbol::Diamond (diamonds), QwtSymbol::Ellipse (circles), QwtSymbol::Hexagon (hexagons), QwtSymbol::HLine (lines), QwtSymbol::LTriangle (left-sided triangles), QwtSymbol::RTriangle (right-sided triangles), QwtSymbol::Star1, QwtSymbol::Star2 (stars) and so on.
You can color the symbols - the logic is the same as in graphs and histograms:
symbol->setBrush(QBrush(QColor(100,200,150)));
symbol->setPen(QPen(QColor(50,50,50)));
We get:
Unfortunately, there is no support for creating bubbles in the scale of QwtPlot with QwtPlot tools. But you can write your own not very difficult function for drawing at least circles.
I managed to create the following:
QVector<QPointF> circle(float x, float y, float r){
QVector<QPointF> vector1;
for (float i = 0; i <= 3.14/2; i += 0.1){
sin(qSin(i));
cos(qCos(i));
vector1.append(QPointF(x + r*cos, y + r*sin));
vector1.append(QPointF(x + r*cos, y - r*sin));
vector1.append(QPointF(x - r*cos, y + r*sin));
vector1.append(QPointF(x - r*cos, y - r*sin));
}
return vector1;
}
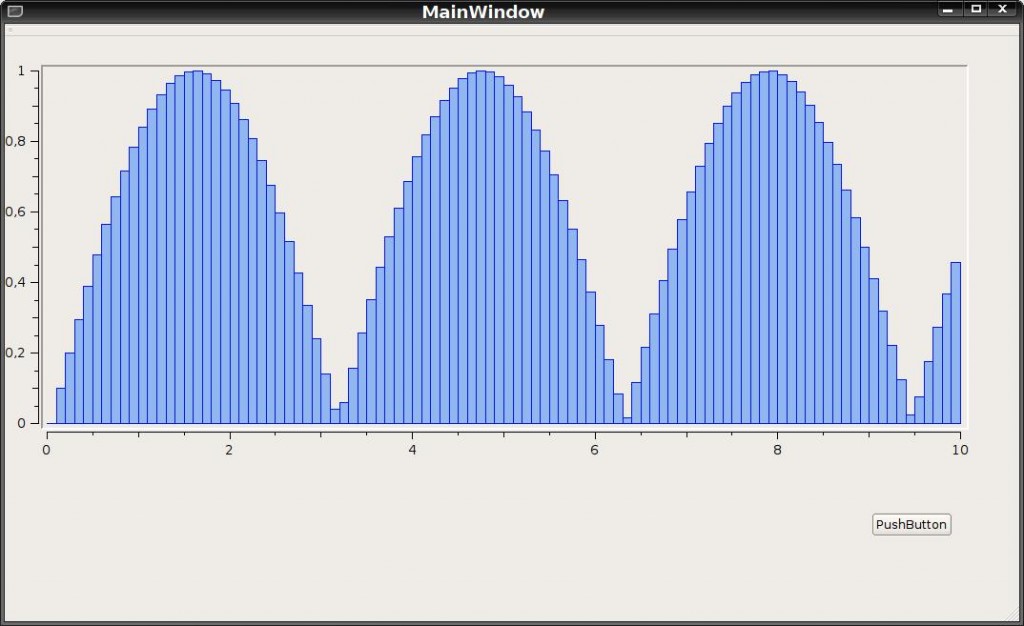
The input parameters of the function are the position x, y of the circle and its radius r in the scale of QwtPlot. The function can be useful for modeling, for example, gas, taking into account the radius of atoms.
If you tweak it a little bit, you can also add the ability to draw other shapes on the QwtPlot scale.
The function returns a vector that contains the points of the circle. You can control the fill density and other parameters by adjusting the function. It is worth noting that it is slightly optimized - since sine and cosine are quite heavy functions, we calculate them only once at each step of the loop, and the values only from 0 to ?/4 are displayed and mirrored.
Now, to plot the circles, in the loop for adding points to the QVector, write:
for (float i = 0; i <= 10; i += 0.1)
points->operator+=(circle(i ,qSin(i), 0.1));
We get: